Impact on Expected Duration, Criticality, and Finish Time Correlation
Schedule simulation can be used to estimate project duration. In addition, it can measure how much a task’s scheduling will influence project duration. Two such measures are a task’s criticality and finish time correlation. Criticality measures the likelihood that a task will appear on a critical path. Finish time correlation measures the relation between a task’s finish time and the project schedule’s finish time.
These three measures, expected project duration, task criticality, and finish time correlation, can vary markedly depending upon whether the simulation takes resource constraints into account. Hence, it is important that a project manager be able to assess the differences that might exist between a resource unconstrained and constrained simulation. I’d like to share below how a resource constrained schedule simulation exposes these differences.
An Example
The figure below shows a project schedule with over allocated resources. It is unleveled. There is one unit of each resource type. This schedule was simulated in two modes: resource unconstrained (resource constraints ignored) and resource constrained (resource constraints enforced). Each simulation included 10,000 trials.
Task durations were randomly sampled from a PERT distribution and based on a three-point estimate of optimistic, most-likely, and pessimistic durations for tasks. In this example, these three task duration estimates were set arbitrarily to 80%, 100%, and 150% of the original task duration estimate.
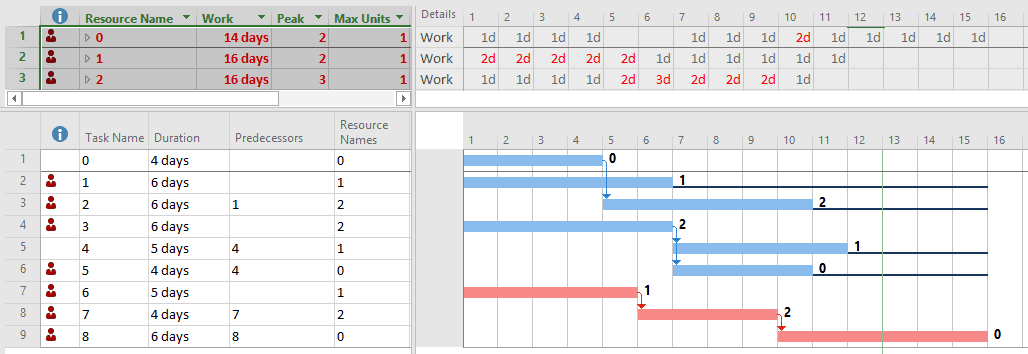
Figure 1. An example showing an over allocated (unleveled) project schedule. Note the critical path = (6, 7, 8) and duration = 15 days.
Expected Duration
The next figure shows two charts: the frequency distributions of project durations from the resource unconstrained and constrained simulations, and the means and cumulative frequency distributions of project durations from the resource unconstrained and constrained simulations. The expected project duration shifts from 15.76 days in the resource unconstrained simulation to 22. 59 days in the constrained simulation. This shift is caused primarily by the imposition of resource constraints.
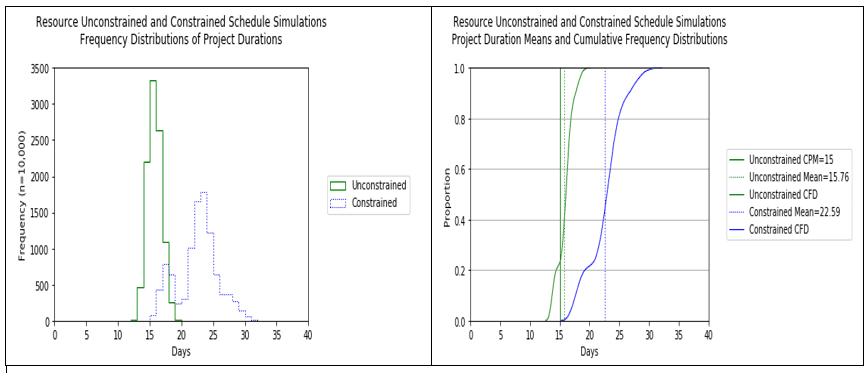
Figure 2. Differences in expected project duration between unconstrained and constrained simulations
Criticality
A task’s criticality is the proportion of simulation trials in which the task is a member of a critical path or resource critical path. It represents the likelihood that the task is critical. We see in Figure 3 the proportions from the resource unconstrained and constrained simulations.
In this particular resource unconstrained simulation, the critical path was (6, 7, 8) in 99.16% of the trials. This is reflected in the criticality of those tasks. However, in the resource constrained simulation, there were 59 unique sets of resource critical paths determining project duration. In this particular sampling, the set [(6,7,8)] was not one of them! The dominant resource critical path set [(3,2,7,8)] determined the project duration in 53.66% of the trials. This is reflected in the resource constrained task criticalities. The four tasks in the dominant resource critical path occurred in other resource critical path sets, as well.
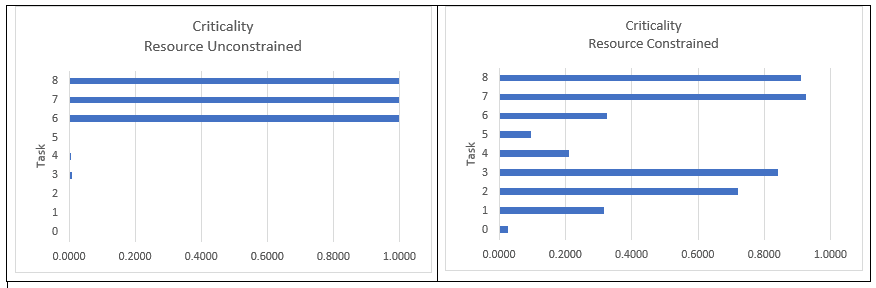
Figure 3. This diagram shows criticality proportions for resource unconstrained and constrained simulations (n=10,000).
Finish Time Correlation
For each trial in the simulation, task finish times and the project finish time were recorded. Spearman’s rank order correlation coefficients were calculated to measure the relationship of task and project finish times in the simulation sample. Since the relationship between a task’s finish time and the project finish might not be linear, a rank order correlation statistic was used. The figure below charts the correlation coefficients for each task.
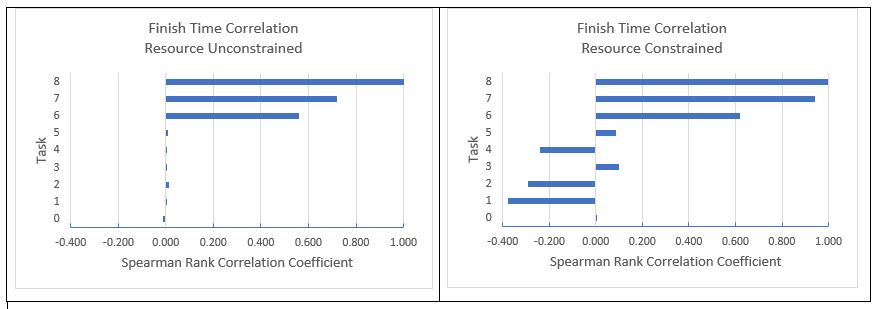
Figure 4. Finish time correlations for resource unconstrained and constrained simulations (n=10,000) are shown.
In the resource unconstrained simulation, the finish times of tasks 6, 7, and 8 were positively correlated with the overall project finish time. When these tasks finished later, the project finished later. These tasks were members of the dominant unconstrained critical path. In the resource constrained simulation, the finish times of tasks 6, 7, and 8 were positively correlated with the overall project finish time. In addition, task 1 had a moderate negative correlation. In trials where task 1 was scheduled earlier, the project finished later. Tasks 2 and 4 had negative correlations, also. In trials where task 2 was scheduled later, the project finished earlier. When task 4 was scheduled earlier, the project finished later.
Conclusions
By looking at this example, we can see that there can be differences between simulation results depending on whether a schedule was resource unconstrained or constrained.
- The expected project duration was greater in the set of resource constrained schedules than in the resource unconstrained schedule, primarily due to the imposition of resource constraints.
- Whereas task criticality mirrored the dominant critical path in the resource unconstrained schedule, it mirrored the dominant resource critical path in the set of constrained schedules.
- Finish time correlations were aligned with the dominant critical path in the unconstrained case, but there were both postive and negative correlations in the resource constrained case, involving tasks not aligned with the dominant resource critical path.
In presenting project duration estimates, it is prudent for a project manager to assess the impact that resource constraints have on expected project duration, task criticality, and task finish time correlation. Resource constrained schedule simulation helps us do this.









Sam Huffman
Masterful treatment of criticality!
Robin Nicklas
Kevin,
Thank you for your question.
The data presented in this article were generated using programs coded in Python and written for the purpose of illustrating the differences in simulation results between resource unconstrained and constrained schedules.
There are several add-in programs for MS Project that run schedule and cost simulations. However, to my knowledge, these add-ins do not take resource constraints into account. The simulation results generated by these add-ins are based on the unconstrained schedule or, at best, only a single instance from the set of resource-feasible schedules.