 Decisions and uncertainties abound in life. Take something as simple as deciding where to go for a short vacation. Do you go to a nearby mountain because your friends like it or to a faraway beach because you like it? The option of staying near the beach may be cheaper but would require a longer travel time, whereas going to the mountains may be a bit expensive, but you’ll arrive there earlier! Which option would you to take?
Decisions and uncertainties abound in life. Take something as simple as deciding where to go for a short vacation. Do you go to a nearby mountain because your friends like it or to a faraway beach because you like it? The option of staying near the beach may be cheaper but would require a longer travel time, whereas going to the mountains may be a bit expensive, but you’ll arrive there earlier! Which option would you to take?
Or say you’re remodeling your house, and you’re choosing between two contractors. Contractor A will cost more than Contractor B. But B isn’t known to be a stickler for time, and there will be a high chance (or probability) for delay, whereas Contractor A, though comparatively expensive has a greater chance of finishing the work on time. Which contractor would you choose?
In both situations uncertainties exist with respect to investment and time. While making your decision, you’ll carefully consider the alternatives and see the possible outcomes. It’s likely that you’ll choose the outcome with the highest value or the one having the least negative impact.
Uncertainties lead to risks. Before taking actions on risks, you analyze them both qualitatively and quantitatively, as we’ve explored in a previous article. By quantifying the risks, you gain confidence.
Let’s take the second situation and quantify it. Let’s say that Contractor A will cost you $50,000 and has a 10 percent chance of coming in late whereas Contractor B will cost you far less — $35,000 — but with a 25 percent chance of being late. For being late, the penalty on either contractor is $10,000. With this information, is it not easier for you to decide which one to hire?
Projects behave in a similar fashion. They’re executed in uncertain environments, whether related to scope, schedule, budget, resources or something else. And like daily life, projects also must be executed despite their uncertainties and risks. If you quantify the risks, decision making becomes much easier.
For quantitative risk analysis, decision tree analysis is an important technique to understand. For your preparation of the Project Management Institute® Risk Management Professional (PMI-RMP)® or Project Management Professional (PMP)® examinations, this concept is a must-know.
Expected monetary value (EMV) analysis is the foundational concept on which decision tree analysis is based. What does EMV do? Let’s work through an example.
Expected Monetary Value (EMV) Analysis
First, don’t confuse EMV with the term EVM! The latter stands for earned value management, whereas EMV stands for expected monetary value, which is completely different. EMV is a tool and technique for the “Perform Quantitative Risk Analysis” process (or simply, quantitative analysis), where you numerically analyze the effect of identified risks on overall project objectives.
The formula for EMV of a risk is this:
Expected Monetary Value (EMV)
= Probability of the Risk (P) * Impact of the Risk (I)
or simply,
EMV = P * I
EMV calculates the average outcome when the future includes uncertain scenarios — positive (opportunities) or negative (threats). Opportunities are expressed as positive values, while threats have negative values. Both the values will be considered by adding them together.
Example: There’s a negative risk (or threat) with a 10 percent probability of prohibiting the execution of a work package. If that risk happens, the impact of not executing the package is estimated at $40,000. For the same work package, there’s a positive risk with a 15 percent probability and impact estimated at a positive $25,000. Should you execute the work package?
Answer:
EMV for the threat = P * I = 10% * (-$40,000) = -$4,000
EMV for the opportunity = P * I = 15% * (+$25,000) = $3,750
Now, the EMV = – $4,000 + $3,750 = -$250
Obviously, you don’t want to execute the work package, because you’ll lose money on it. When a work package or activity is associated with a risk, you can find the individual EMV. In other words, you quantify the individual risks.
That covered EMV for an individual work package. How about the overall project risk? A project, after all, will have many work packages, right?
To figure this out, you calculate the EMV by multiplying the value of each possible outcome (impact) by its likelihood of occurrence (probability) and then adding the results — which leads us back to our original topic. A common use of EMV is found in decision tree analysis.
Decision Tree Analysis
Decision tree analysis (DTA) uses EMV analysis internally. A decision tree, as the name suggests, is about making decisions when you’re facing multiple options.
Here are some of the key points you should note about DTA:
- DTA takes future uncertain events into account. The event names are put inside rectangles, from which option lines are drawn.
- There will be decision points (or “decision nodes”) and multiple chance points (or “chance nodes”) when you draw the decision tree. Each point has different symbols: a filled up small square node is a “decision node”; a small, filled-up circle is a “chance node”; and a reverse triangle is the end of a branch in the decision tree. These are noted in this table:
| Notation | Shape | Meaning |
|---|---|---|
| Filled-up square | Decision node | |
| Filled-up circle | Chance (condition) node | |
| Reverse triangle | End of branch |
- Because this format results in a diagram that resembles a tree branching from left to right, decision tree is an apt name!To analyze a decision tree, move from left to right, starting from the decision node. This is where the branching starts. Each branch can lead to a chance node. From the chance node, there can be further branching. Finally, a branch will end with end-of-branch symbol.
- The probability value will typically be mentioned on the node or a branch, whereas the cost value (impact) is at the end.
- Next come the calculations on the branches of the tree. To calculate, move from right to left on the tree. The cost value can be on the end of the branch or on the node. Just follow the branch to do the calculation.
- The best decision is the option that gives the highest positive value or lowest negative value, depending on the scenario.
Let’s work through an example to understand DTA’s real world applicability.
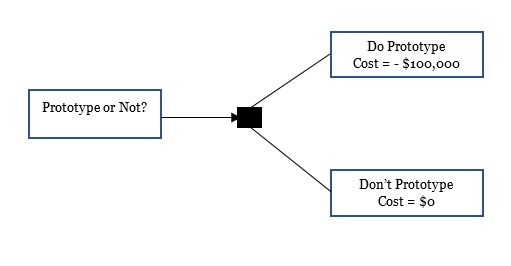
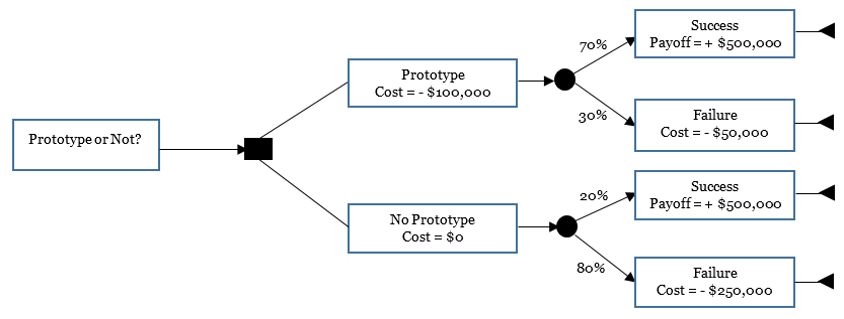
Example: You’re doing a prototype for your project, but you’re not sure whether to proceed with this prototype. If you do the prototype, it will cost you $100,000; and, of course, if you don’t pursue it, there will be no cost. If you do the prototype, there is 30 percent chance that the prototype might fail, and for that the cost impact will be $50,000. However, if the prototype succeeds, the project will make $500,000. If you do not do any prototype, you’re already taking a risk, the chance of which is 80 percent with a failure impact of $250,000. But, again, without a prototype, should you succeed, the project will make the same money as mentioned before. What should you do?
Answer:
To begin your analysis, start from the left and move from the left to the right. First, draw the event in a rectangle for the event — “Prototype or Not.” This obviously will lead to a decision node (in the small, filled-up square node as shown below).
From there, you have two options — “Do Prototype” and “Don’t Prototype.” They are also put in rectangles as shown below.
Each option will lead to two events or chances — success or failure — branching out from the chance nodes. Taking the first option, if it fails, which has a 30 percent chance, the impact will be $50,000. If it succeeds (a 70 percent chance), there’s no cost, but there is a payoff of $500,000. These are noted on the arrows. Similarly, for the second decision, “Don’t Prototype”:
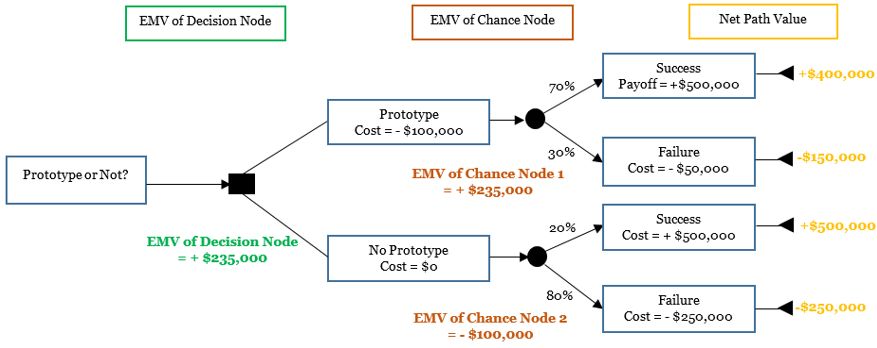
By looking at it, can you conclude anything? I can’t. So let’s do the EVM analysis. To calculate, as noted before, you move from right to left. First, calculate the net path value along each branch of the decision tree. The net path value for a path over the branch is the difference between payoff minus costs. Next, at every chance node, calculate the EMV. From these EMVs, we can find out the EMV of at the decision node. The decision giving the highest positive value or lowest negative value is selected.
This is summarized in this table.
| Decision definition | Decision node | Condition (or chance) node | Net path value |
|---|---|---|---|
| Decision to be made | Input: Cost of each option Output: Decision made Decision node is a black rectangle or square. | Input: Scenario probability, reward or penalty if it occurs. Output: EMV Chance node is a circle. | Computed cost: Payoff minus costs along the path. End path is shown with a reverse arrow mark. |
EMV for Chance Node 1, the first circle:
The net path value for the prototype with 70 percent success = Payoff – Cost:
= +$500,000 – $100,000
= +$400,000
The net path value, for the prototype with a 30 percent failure = Payoff – Cost:
= -$50,000 – $100,000
= -$150,000
EMV of chance node 1 = [70% * (+$400,000)] + (30% * (-$150,000)]
= +$280,000 – $45,000
= +$235,000
EMV for Chance Node 2 (the second circle):
The net path value for the prototype with a 20 percent success = Payoff – Cost:
= +$500,000 – $0
= +$500,000
The net path value for the prototype with 80 percent failure = Payoff – Cost:
= -$250,000 – $0
= -$250,000
EMV of chance node 2 = [20% * (+$500,000)] + (80% * (-$250,000)]
= +$100,000 – $200,000
= -$100,000
These results are shown in this figure:
Which alternative would you take? Look at the EMV of the decision node (the filled-up square). That’s +$235,000. With the other option — no prototyping — you’re losing money. Hence, you should go for the prototype.
Decision tree analysis can be applied to various project management situations where you’re faced to options or alternatives.
Coming back to the example of the house remodel, can you now say which vendor to choose? You can draw a diagram like the previous ones, or you can do a quick calculation:
For Contractor A, the cost will be:
Pay cost + Payback for delay
= (-$50,000) + 10% * ($10,000)
= -$50,000 + $1,000
= -$49,000
For Contractor B, the cost will be:
Pay cost + Payback for delay
= (-$35,000) + 25% * ($10,000)
= -$35,000 + $2,500
= -$32,250
The best answer? With the available data, you’d go with Contractor B, even though this vendor has a higher chance of being delayed.
It’s worth noting that the application of decision tree analysis isn’t only limited to risk management. DTA can be applied to machine learning for artificial intelligence (AI) and data mining in big data analytics.
Go forth and calculate your way to better decisions!








Sri
Very good explanation.
Wondering why in case of contractor example path values are not calculated. For example, contractor A’s final cost comes to $40,000 (pay cost – payoff when late = $50,000 – $10,000 = $ 40,000) which happens only 10% time. So the EMV of that choice node is 40,000 x 0.1 = $4,000.
Please explain.
Thank you,
Sri
sparsha
cant understatnd this pleace give slear information about the decetion tree anaylsis
pmp aspirant
Thankyou for the article . well explained