Sequencing Product Backlog

When modeling a project as a flow process, one objective is to deliver the maximum amount of value in the shortest amount of time. Most project managers likely start with an inventory of features in a product backlog. The sequence in which features are executed determines whether we will achieve the objective. The effectiveness of the sequencing depends upon the interaction of three process variables:  flow rate, flow time, and the inventory of work in progress (WIP).

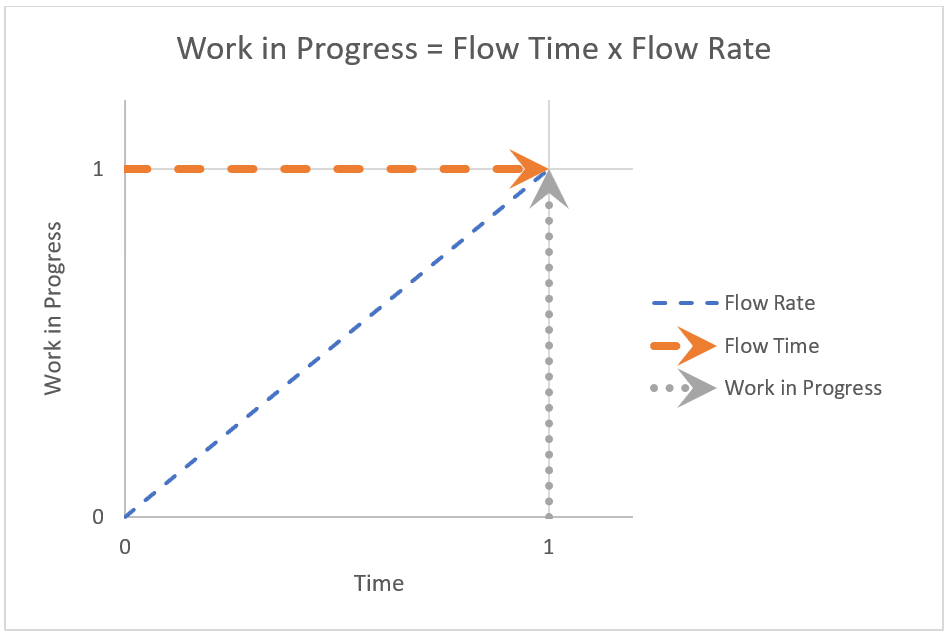
The graph below illustrates the fundamental relationship of these variables. It exemplifies Little’s Law, which states that average work in progress equals the product of average flow rate and average flow time (Cahon and Terwiesch, 2013). Flow time is the horizontal distance. The inventory of WIP is the vertical distance. Flow rate is the slope (WIP / flow time). The greater the slope, the more work is accomplished per time period. If you want to maximize the value of work delivered in the shortest amount of time, you’ll want to sequence features by monotonically decreasing flow rate.

Figure 1. Little’s Law

The inventory of WIP can be measured in a variety of ways. The simplest way is to consider a feature to be the flow unit and to count the number of incomplete features in the process at any time. However, some features may be more important or valuable than others. If those features are weighed according to their potential revenue or cost savings upon completion, then one can assess the value of the WIP inventory using a dollar as the flow unit. If we do not claim a feature’s value until it is completed, then the value is delayed by the flow time of the feature or the amount of time it spent in the process. The flow time of a feature weighted by its dollar value is considered a delay cost. For the sake of a sequencing example, let’s assume we want to minimize the value-weighted flow time of the process. In other words, we want to minimize delay costs.

Start with a Simple Product Backlog . . .

The table below shows a product backlog with five features. Processing times and value weights have been assigned arbitrarily. Processing time (duration) is a proxy for the amount of work or cost required to complete a feature. Here, we will measure it in weeks. Feature 4 has the shortest duration and feature 5 has the longest. A feature’s value is the potential revenue or savings realized once the feature is complete. Feature 1 is the most important and feature 5 is the least, in terms of dollar value. All features are available for execution at the start of the process. That is, their release times are zero.

Table 1. Example product backlog of features with processing times, release times and value weights.

Let’s make two simplifying assumptions. First, the development team can only work on one feature at a time. This limits our discussion to the “single machine” model. With only one resource (i.e., the team), the makespan of the process will be 19 weeks, which is the sum of all of the processing times. Secondly, we are assuming the flow rate at which the team works remains constant. The total value of the features in the product backlog is $212,000. The average flow rate is $11,158 per week.

How Should We Sequence the Backlog?

Let’s look at three scenarios. Reinertsen (2009) suggests that if we are indifferent to processing times, we would sequence the features in decreasing order of value. The most valuable features are completed first. If we are indifferent to value, we would sequence the features in increasing order of processing time. In this case, the shortest features are completed first in order to minimize average flow time. When both processing time and value are important, the features should be sequenced in decreasing order of weighted processing time, the quotient of value and processing time. Features that deliver the most value per processing time are completed first in order to minimize average weighted flow time.

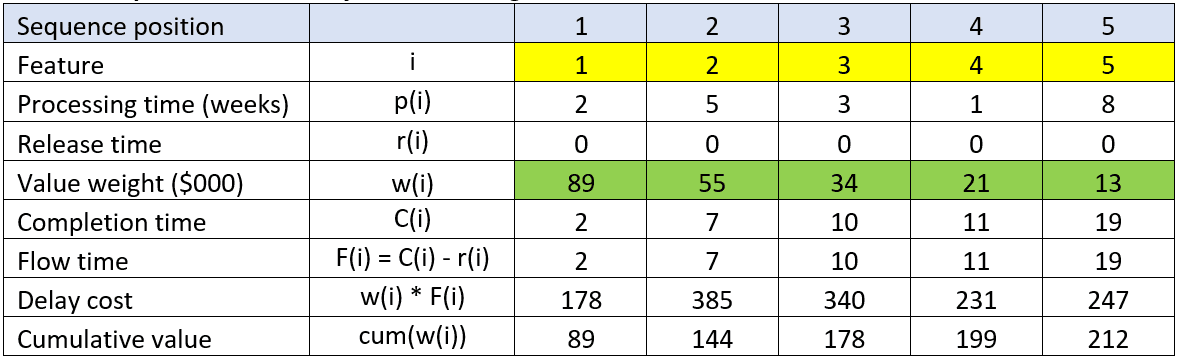
Scenario 1: Most Valuable Feature First

If we sequence the features based only on value, the result is shown in Table 2 below. The sequence position is determined according to the decreasing order of value weights (w(i)). Reinertsen calls this Highest Delay Cost First (HDCF) sequencing. C(i) is the completion time for each feature. Feature 1 was released to the process at time 0, started at time 0, and completed at time 2. Feature 2 was released to the process at time 0, started at time 2, completed at time 5, and so forth. The flow time F(i) for each feature is the difference between the feature completion time and the feature release time (C(i) – r(i)). It represents the total time the feature was in the process, including any waiting time prior to execution.

The delay cost for a feature is the product of its flow time and value weight (w(i) * F(i)). It represents how long we had to wait for that feature’s value to be delivered.

The average flow time for a feature is 9.8 weeks. The total cost of delay is $1,381,000.

Table 2. Sequence based solely on decreasing value

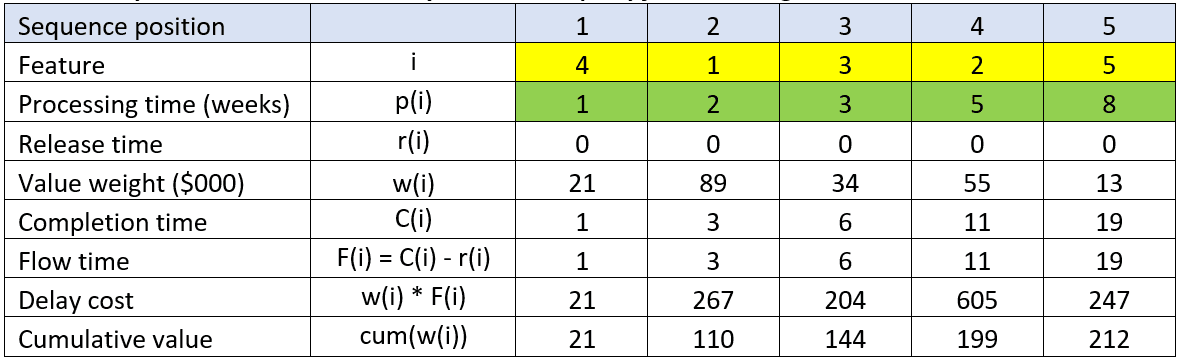
Scenario 2: Shortest Processing Time First

If our goal is to minimize the average flow time (the amount of time a feature takes to complete), we would sequence features in increasing order of process times. This is known as shortest processing time (SPT) sequencing (Baker and Trietsch, 2009). Reinertsen calls this Shortest Job First (SJF). Table 3 shows the result of this ordering.

The average flow time for a feature is 8 weeks and the total cost of delay is $1,344,000. This will be the shortest average flow time of the three scenarios presented here. Note that the total cost of delay has decreased compared to the first scenario.

The result can be verified by using Excels’ Evolutionary Solver. The objective function is to minimize the sum of flow times by permuting the feature sequence.

Table 3. Sequence based on shortest process time (SPT) first ordering

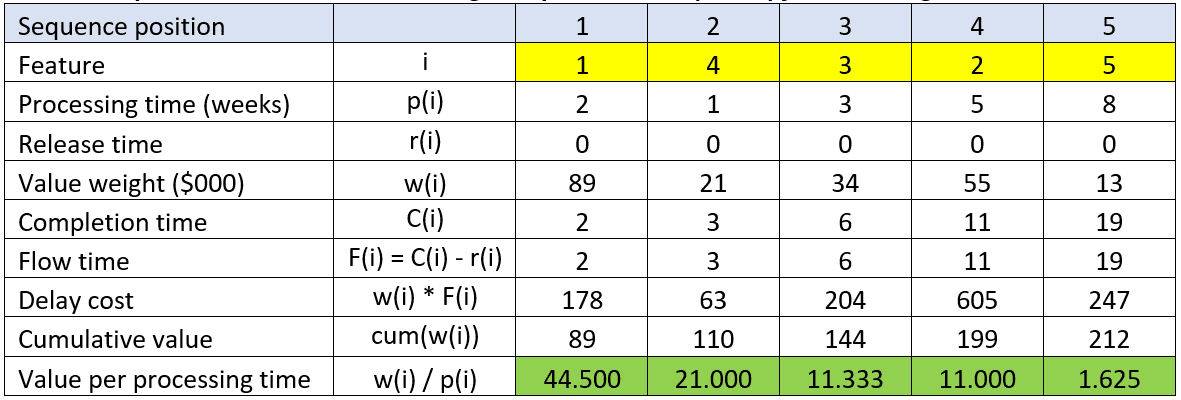
Scenario 3: Shortest Weighted Processing Time First

If our goal is to deliver maximum value within the shortest time, we would sequence features in decreasing order of value per processing time. This is known as shortest weighted processing time (SWPT) sequencing (Baker and Trietsch, 2009), although Reinertsen refers to it as Weighted Shortest Job First (WSJF) sequencing. Reinertsen’s nomenclature was adopted by the Scaled Agile Framework – Enterprise (SAFe) methodology (Weighted Shortest Job First). Cohn (2005) describes a “relative weighting” technique for sequencing a product backlog, which is similar to what we describe here.

In this scenario, the average feature flow time increased slightly to 8.2 weeks, but the total delay cost decreased to $1,297,000, which is the minimum total delay cost of the three scenarios presented.

As above, the result can be verified by using Excel’s Evolutionary Solver. The objective function is to minimize the sum of weighted flow times by permuting the feature sequence.

Table 4. Sequence based on shortest weighted process time (SWPT) first ordering

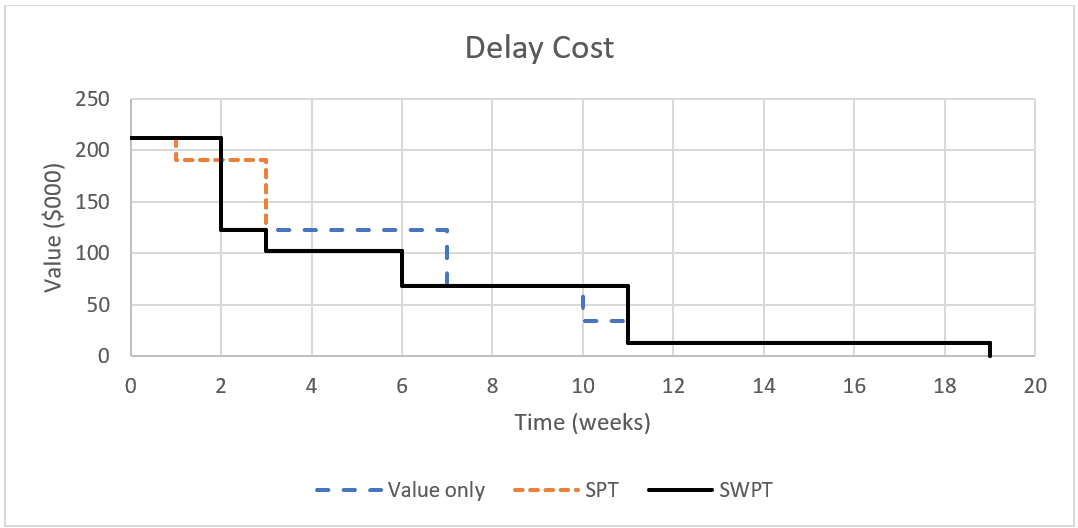
Figure 2 shows the delay cost curves for the three scenarios presented above. The area under the SWPT curve is the least of the three scenarios.

Figure 2. Delay cost curves for value only, SPT and SWPT sequencing.

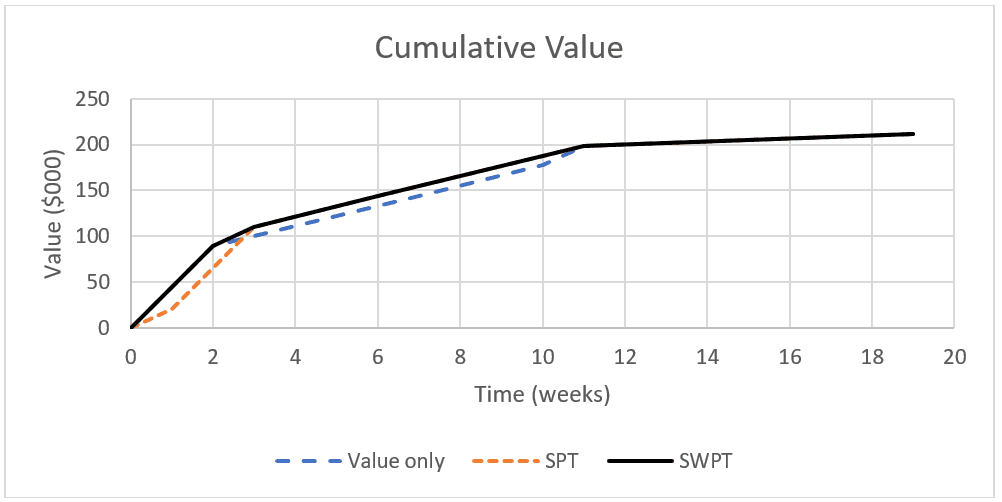
Figure 3 below shows the cumulative value delivered. The slope of the SWPT curve decreases monotonically, whereas the other curves do not.

Figure 3. Cumulative value delivered for value only, SPT and SWPT sequencing.

Little’s Law Revisited

At the start of this article, I stated that the effectiveness of sequencing depended upon the interaction of three process variables:  inventory, flow rate, and flow time. Little’s Law states that in a flow process average WIP inventory equals the product of average flow time and average flow rate. The table below shows the value of these variables across all three scenarios discussed above.

Table 5. Scenario flow variable averages

The flow unit is one dollar. Flow rate is a constant $11,158 per week ($212,000 / 19 weeks). Average value of WIP can be computed by evaluating the delay cost during each week in the process makespan. Little’s Law enables the computation of average flow time using the average flow rate and average WIP value. Shortest weighted processing time (SWPT) sequencing provides the lowest average flow time and average WIP costs.

References

Baker, Kenneth R. and Trietsch, Dan. 2009. Principles of Sequencing and Scheduling. Wiley. Pp. 15-21.

Cahon, Gerard and Terwiesch, Christian. 2013. Matching Supply with Demand: An Introduction to Operations Management, 3^rd ed. McGraw-Hill Irwin. Pp. 15-19.

Cohn, Mike. 2005. Agile Estimating and Planning. Prentice-Hall. Pp. 117-119.

Reinertsen, Donald G. 2009. The Principles of Product Development Flow:  Second Generation Lean Product Development. Celeritas Publishing. Pp.191-198.

Weighted Shortest Job First. www.scaledagileframework.com/wsjf/