 Imagine this scenario. You are going to a friend’s house for an important event. It is scheduled with a hard start, meaning you can’t have delays, but as you start traveling, you notice that your vehicle is running low on gasoline. A few options come to mind:
Imagine this scenario. You are going to a friend’s house for an important event. It is scheduled with a hard start, meaning you can’t have delays, but as you start traveling, you notice that your vehicle is running low on gasoline. A few options come to mind:
- Continue driving because you think your available gasoline will suffice.
- Fill-up your gasoline tank at a nearby gas station and then continue to travel.
- Use a small gasoline container you have with you to fill-up your tank and then continue to travel.
Which option would you choose? What impact will your choice have for the duration of your trip? Can you reach your friend’s house on time?
These questions lead to a concept called probabilistic branching and analysis, which is used in quantitative risk analysis and management. Probabilistic branching is one of the ways to represent individual project risks. In every probabilistic branch, you model individual project risks and determine the overall project risk.
In this article, we’ll start with the fundamental concepts used in probabilistic branching. I’ll illustrate them with an example, show how to build a project plan with MS Project, help you create the needed probabilistic branching, and provide analysis and interpretations. In conclusion, we will see the significance of this concept.
Uncertainty in Schedule Network Diagram
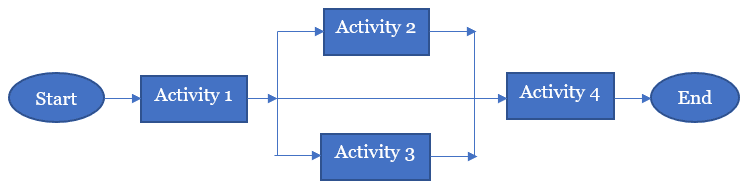
If you consider the options you had running low on gasoline while driving to your friend’s house, a simple network diagram can be built:
- Start (milestone) – Starting from your home
- Activity 1 – Starting to travel in your vehicle
- Activity 2 (an option or branch) – Fill-up the tank at a nearby gas station
- Activity 3 (another option or branch) – Use the small gas container available
- Activity 4 – Continue travelling
- End (milestone) – Reach your friend’s house
This seems pretty straightforward, but can you be sure of which option or branch you should take considering your desire to arrive at your friend’s house on-time? It may not be as straightforward as you think due to these activities being uncertain (may or may not happen). Uncertainties mean risks, and these risks can ultimately impact your objective (reaching your friend’s home on-time for the event). Hence, you can give probability or chance of occurrence to these risks on each of the branches.
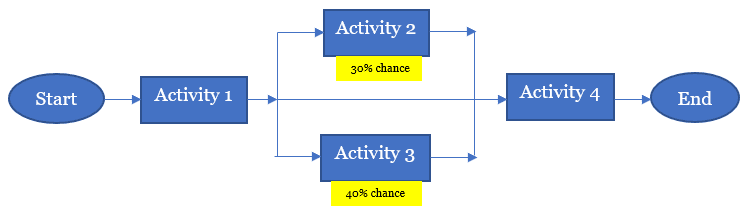
When you assign probability values to each branch, you get a risk-adjusted schedule network diagram. We can modify our previous network diagram and represent as shown:
For “Activity 2” and “Activity 3,” I’ve assigned 30% and 40% chances, respectively, as existence values.
As you assign probability values to individual branches in response to the risks, the branches in the network diagram are known as probabilistic branches. You can have single or multiple probabilistic branches, though the latter is more frequently used.
Statistically Independent
Consider closely our first example:
Can you take two options or go for two branches simultaneously? In other words, would you fill-up the tank at a nearby gas station and use the small gas container available?
Obviously, you would not, as it doesn’t add any value for you. In fact, these are two independent outcomes–more specifically these outcomes are statistically independent. When you build a schedule network diagram (as shown in previous figure) with probabilistic branches, you model the risk of different outcomes occurring in a project in each branch.
Therefore, you could say probabilistic branching is best used when the risks occurring are statistically independent, meaning that one risk occurring in one branch is statistically independent of another risk occurring in another branch.
With this background and fundamentals explained, let’s look now at a real-time, project management example and get a bit deeper into probabilistic branching and analysis.
An Example
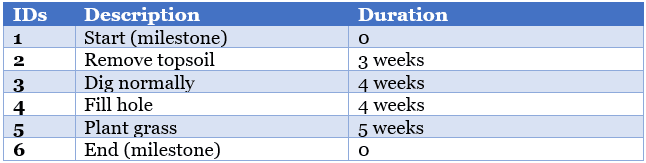
Let’s say that you and your team are excavating in an area to have a new garden prepared for a town’s residents. Your team will remove the soil, dig normally, then fill the hole, and finally plant grass to complete the work.
The tasks in this project will occur as shown in the below table. I’ve added duration details for each task or activity. Note that this example is taken from Primavera tutorial and modified with respect to MS Project usage and respective representations in this article.
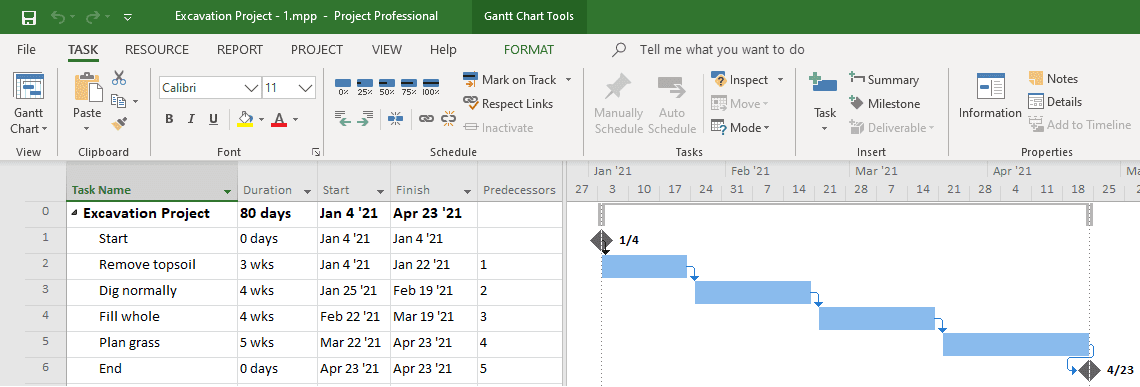
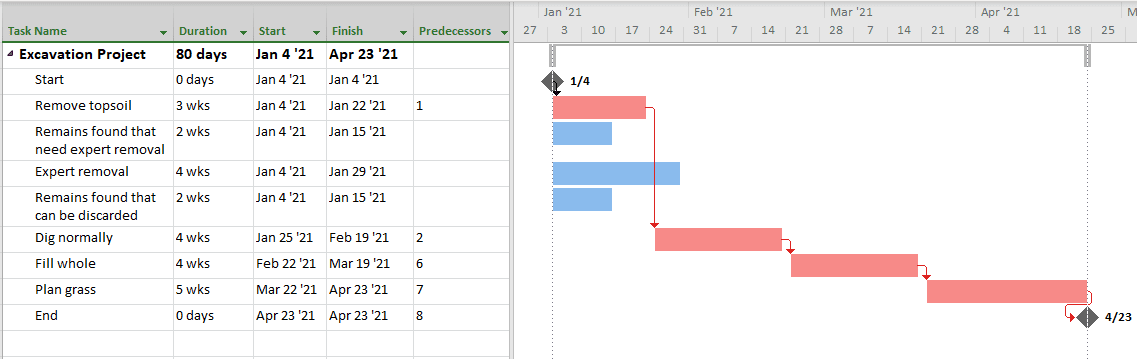
What good can a project plan be, if we don’t know the total duration and end date? In such a case, scheduling software comes to our aid. Using Microsoft Project software, the plan looks as shown below.
The project is starting on January 4, 2021 and finishing on April 23, 2021. The duration is calculated to be 80 days.
So far, so good. There is no difficulty at all in creating a plan for this simple project.
But, as with many projects we manage, we have a twist!
Decide on the Branches
Let’s say that you get in touch with local experts and are informed of a possibility of archaeological remains in the area. Obviously, you just can’t go on and just start digging in this scenario. You may think of three possible scenarios or outcomes.
- Archaeological remains need expert removal.
- Archaeological remains can be discarded.
- No actual archaeological remains are found.
These scenarios can be modelled using probabilistic branching with three branches for three possible types of outcomes. All these outcomes, as you can see, are statistically independent.
Now, because these are probabilistic branches, there will be risks associated with each branch. At this point, we can confidently say the following:
- Risk 1 (on Branch 1):
- Archaeological remains are found that need expert removal.
- Chance of occurrence (probability value) = 5%
- Risk 2 (on Branch 2)
- Archaeological remains are found, but can be discarded.
- Chance of occurring = 25%
- Risk 3 (on branch 3)
- No archaeological remains are found.
- Chance of occurring = 70%
As you see above, a probability value is assigned to each outcome or branch. You can decide on the probability values to be assigned subjectively and/or with expert opinion.
Add New Tasks to the Plan
Before we perform a risk analysis, we need to include all three of the above branches into the existing plan. In our plan, we have three new tasks representing the three outcomes or branches. The new tasks, along with existing tasks in the plan are:
- Task – 1: Remove topsoil
- Task – new: Remains found that need expert removal
- Task – new: Expert removal
- Task – new: Remains found but can be discarded
- Task – 2: Dig normally
- Task – 3: Fill hole
- Task – 4: Plant grass
Did you notice the branching that occurred after the “Remove topsoil” task? After this task, we now have three possibilities or three branches: “Remains found that need expert removal,” “Expert removal,” and “Remains found but can be discarded.”
Next, let’s add these tasks to our MS Project plan with the following durations:
- Remains found that need expert removal = 2 weeks
- Expert removal = 4 weeks
- Remains found that can be discarded = 2 weeks
After this step, we see the following modified plan within MS Project.
As shown in the above figure, with the addition of the new tasks, there is no change in the project duration, the critical path, or the finish date. However, we are not done with our plan yet.
Link the Tasks to the Existing Tasks
We have to link the newly inserted tasks and include the probabilistic branching for each of these tasks. I’ll be linking the tasks as follows:
- Link the finish of “Remove topsoil” task to the start of “Remains found that need expert removal” task.
- Link the finish of “Remains found that need expert removal” task to the start of “Expert removal” task.
- Link the finish of “Expert removal” task to the start of “Fill hole” task.
- Link the finish of “Remove topsoil” task to the start of “Remains found but can be discarded” task.
- Link the finish of “Remains found that can be discarded” task to the start of ‘Fill Hole” task.
Logically, the above sequence makes sense. For example, if you remove the soil and require expert removal, then these tasks should be linked with FS dependency. Next, the task “Expert removal” will be linked to the task “Remains found that need expert removal” and so on.
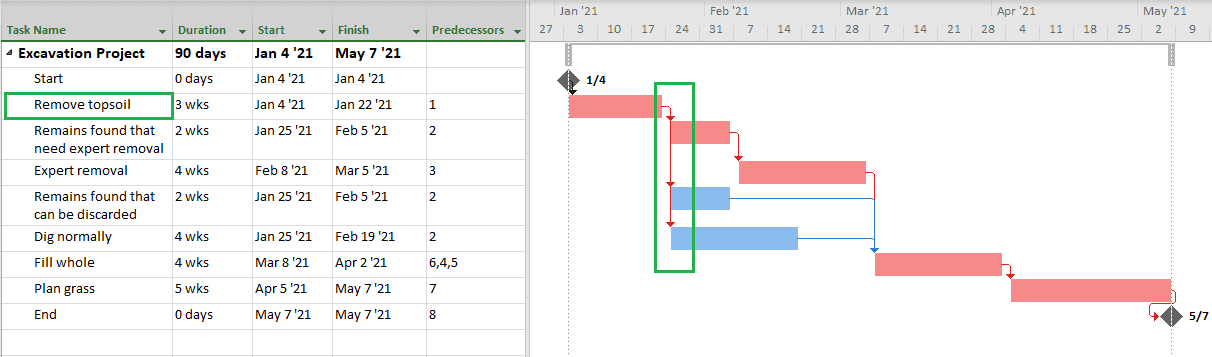
After linking the tasks, the project plan as created with MS Project will result as shown below.
From the task “Remove topsoil,” we have three branches, [v.i.z]:
- “Remains found that need expert removal”
- “Remains found that can be discarded”
- “Dig normally”
The branching from the “Remove topsoil” task has been highlighted in green in the above figure.
In the above modified plan, the project continues to start on the same date of January 4, 2021, but finishes on May 7, 2021 (it was April 23, 2021). The duration of our project has been recalculated as 90 days (from 80 days) and the critical path for the project has also changed.
Assign Probability to the Branches
Next, we will import this Microsoft project plan (.mpp) file into Primavera Risk Analysis software and assign the probability for each of these branches. We will use the following probability values, which we had decided upon earlier.
- Remains are found that need expert removal – 5%
- Remains found but can be discarded – 25%
- Dig normally – 70%
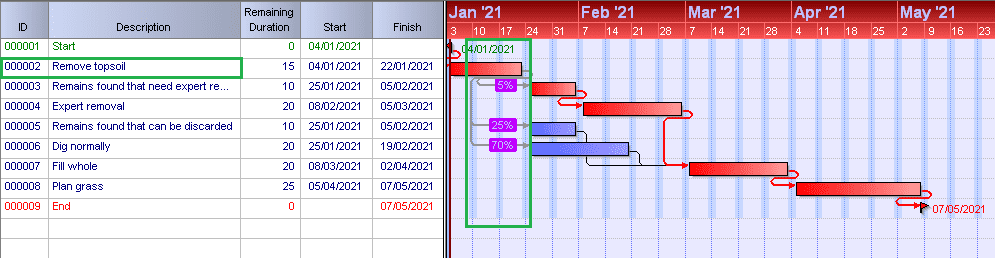
The .mpp file will be seamlessly imported and will be depicted as follows:
This plan is an exact replica of the MS Project plan that we had created before with branching happening from the “Remove topsoil” task (highlighted in green). In each branch, probability values have been assigned, highlighted in the pink color in the graphical side of the Gantt chart and noted to the left of the bars. The critical and non-critical tasks are also the same, highlighted in red and blue colors, respectively.
Run a Risk Analysis
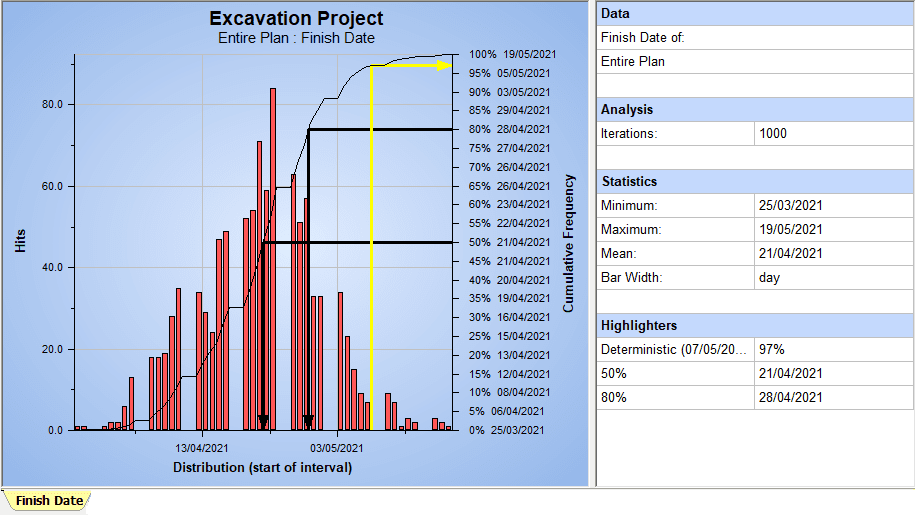
Next, we have to simply run an analysis on the risk adjusted schedule model, and we will iterate the plan a number of times for simulation. The resultant histogram will show as below, post the simulation (known as the Monte Carlo simulation). I’ve formatted the histogram with color coding, highlighted arrow marks, and other data representation.
Let’s interpret the above graph as follows:
- In our initial plan, the project was supposed to be completed by April 23, 2021. In the new plan, after adding the probabilistic branches, the end date moved to May 07, 2021.
- The chance of completing the project by May 07, 2021 is 97%, which is mentioned in the “Highlighters” section in the table to the right. The corresponding line projections are highlighted in yellow arrow marks on the graph.
- The project has a 50% chance of completing by April 21, 2021, and an 80% chance by April 28, 2021. These are highlighted in black (or bold) arrow marks on the graph.
- A 100% chance of completion is possible by May 19, 2021, which is nearly two weeks beyond our planned finish date with probabilistic branches.
Conclusion
Let’s go back to our first example of travel to a friend’s house. It’s not a complex one, and it’s possible that you will be able to calculate the end result in your mind with probabilistic branches.
However, in the real-world, projects or programs are expected to be complex, and you will be needing management and simulation software tools to determine the impact of probabilistic branching to your finish time. To use these software tools, you need to have clarity on probability branching, understanding how to create branches and link with the existing tasks in the plan for analysis.
If you are aspiring to be a Risk Management Professional (RMP), you can expect questions pertaining to these concepts on the exam. On the other hand, if you are an aspiring Project Management Professional (PMP), you need to have a basic understanding on probabilistic branching and how it’s used as a tool, as well as the technique named “Representation of Uncertainty” in quantitative risk analysis.
It is my hope that, within this article, you received a sound understanding on when and why to use probabilistic branching, as well as how run an analysis with an example and hands-on software tools.
References
[1] Book: I Want To Be A RMP, The Plain and Simple Way, Second Edition, by Satya Narayan Dash
[2] Online Course: Practical RMP with Primavera Risk Analysis, Second Edition, by Satya Narayan Dash
[3] Online Course: MS Project Live Lessons, by Satya Narayan Dash








John Owen
Thanks for the article. I am generally suspicious of a risk analysis that shows a better than 50% chance of achieving the schedule deterministic finish. It tends to mean the end is constrained, not properly logically linked, or the uncertainty assumptions are extremely optimistic. In your example I wondered if this was because Activity 5 (Remains found and can be discarded) has a shorter duration than ‘dig normally’ so there’s effectively a 25% chance the project will be completed quicker if remains are found and then discarded. I ran the data in Microsoft Project using our Full Monte with +/-10% duration uncertainty and you can clearly see the three outcomes. ). I reran the analysis increasing the duration of Activity 5 and the chance of achieving the deterministic finish only dropped to 87% (using my uncertainty) so it just shows my suspicious nature isn’t always right :).
Satya Narayan Dash
Thank you John for the comment. Interesting perspective. PMs are pointed out when there are variations in estimates. In a way, it pays to be cautious 🙂 Perhaps, the adage ‘trust and verify’ is better than ‘trust, but verify’. Great to see you have checked hands-on. The end result for deterministic finish, at first glance, seems to be close.
In my simulation, a number of factors/parameters are involved – duration uncertainty (mine was +/-25% in simulation), probabilistic distributions of individual tasks, type of sampling for risk analysis, among others.
Robin Nicklas
Varying task duration in the simulation masks the effect of the probabilistic branching. Per his comment above, John Owen ran a similar simulation, but apparently allowed less variation in task duration. His chart more clearly shows the multimodal nature of the project finish date frequency distribution for this example.
To highlight the effect of probabilistic branching, simplify the simulation by considering only deterministic task durations.
As described in the article, the schedule has three independent and mutually exclusive tasks: remains found but can be discarded (10d, 25% likely), dig normally (20d, 75% likely), and remains found that need expert removal (30d—including the 20d expert removal, 5% likely). The expected duration of the three probabilistic tasks is 18d, a simple weighted average.
If you add in the 60d duration of the constant tasks (remove topsoil, 15d; fill hole, 20d; and, plant grass, 25d), the schedule has three potential paths of 70d, 80d and 90d, respectively. Only one of these paths will be traversed during execution.
The expected project duration is 78d (18d + 60d), or 21 April 2021, which roughly coincides with the mean project finish dates shown in the graph in the article and the chart John provided.
So, one benefit of running the schedule simulation with probabilistic branching is it allows you to estimate the expected project duration.
The real problem lies in deciding which schedule to proffer. If you choose the 90d schedule, it is 95% likely to be an overestimate. If you choose the 80d schedule, it is still 25% likely to be an overestimate. If you choose the 70d schedule, it is 75% likely to be an underestimate. Even using the expected project duration of 78d is not a bet most project managers would be willing to take.
This is where the project finish date cumulative frequency comes into play, as shown in the graph and chart mentioned above. Using it, in conjunction with knowledge of our stakeholders’ risk tolerances and what constraints we are operating under (contract dates, liquidated damages, etc.), allows us to choose the level of uncertainty we are willing to tolerate in our schedule estimates.
Satya Narayan Dash
Task duration can (and will) vary on many aspects. For example, it can vary depending on what stage of the project you are in. It can be +/-10%, 25% or even higher. In the early stages of a project, it can be more. Simulation is not a one-time activity. It can happen multiple times over the project. As duration can vary, of course, there will be impact on the end date and chances (in %) to meet that date. In fact, during Simulation too, task durations will vary as the software iterates over the probabilistic branches.
Coming to the other part, I look at the end goals of simulations not as which schedule to be proffered to the stakeholders, but what is acceptable to the key stakeholders keeping the overall project objectives in mind. Will a 50% chance of meeting the end date be acceptable or will a 80% chance? Which objective(s) they want to protect? What’s the organization’s mandate? The article shows the finish date’s chances (I would prefer a graph which highlights 50%, 80% as can be seen by clicking on the figure, which enlarges. This again is based on organization’s reporting requirements). Similarly, chances can be calculated for duration, float, and other areas. And the way the calculations have been done in the Simulation are different.
Risk tolerance is not much used now in the latest risk management standards that I’ve seen. However, I’m flexible on usage of the term. Nevertheless, based on these standards, in quantitative risk analysis, where probabilistic branching is used, it’s more or less about overall project risk, overall chances of project success, overall project risk exposure etc.